Probability distribution
chi
Probability density function
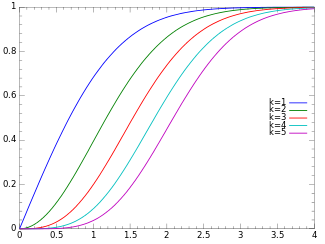
Cumulative distribution function
Notation
χ
(
k
)
{\displaystyle \chi (k)\;}
χ
k
{\displaystyle \chi _{k}\!}
Parameters
k
>
0
{\displaystyle k>0\,}
Support
x
∈
[
0
,
∞
)
{\displaystyle x\in [0,\infty )}
PDF
1
2
(
k
/
2
)
−
1
Γ
(
k
/
2
)
x
k
−
1
e
−
x
2
/
2
{\displaystyle {\frac {1}{2^{(k/2)-1}\Gamma (k/2)}}\;x^{k-1}e^{-x^{2}/2}}
CDF
P
(
k
/
2
,
x
2
/
2
)
{\displaystyle P(k/2,x^{2}/2)\,}
Mean
μ
=
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
{\displaystyle \mu ={\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}}
Median
≈
k
(
1
−
2
9
k
)
3
{\displaystyle \approx {\sqrt {k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}}}}
Mode
k
−
1
{\displaystyle {\sqrt {k-1}}\,}
k
≥
1
{\displaystyle k\geq 1}
Variance
σ
2
=
k
−
μ
2
{\displaystyle \sigma ^{2}=k-\mu ^{2}\,}
Skewness
γ
1
=
μ
σ
3
(
1
−
2
σ
2
)
{\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}
Excess kurtosis
2
σ
2
(
1
−
μ
σ
γ
1
−
σ
2
)
{\displaystyle {\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}
Entropy
ln
(
Γ
(
k
/
2
)
)
+
{\displaystyle \ln(\Gamma (k/2))+\,}
1
2
(
k
−
ln
(
2
)
−
(
k
−
1
)
ψ
0
(
k
/
2
)
)
{\displaystyle {\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi _{0}(k/2))}
MGF
Complicated (see text) CF
Complicated (see text)
In probability theory and statistics , the chi distribution is a continuous probability distribution over the non-negative real line. It is the distribution of the positive square root of a sum of squared independent Gaussian random variables . Equivalently, it is the distribution of the Euclidean distance between a multivariate Gaussian random variable and the origin. The chi distribution describes the positive square roots of a variable obeying a chi-squared distribution .
If
Z
1
,
…
,
Z
k
{\displaystyle Z_{1},\ldots ,Z_{k}}
k
{\displaystyle k}
normally distributed random variables with mean 0 and standard deviation 1, then the statistic
Y
=
∑
i
=
1
k
Z
i
2
{\displaystyle Y={\sqrt {\sum _{i=1}^{k}Z_{i}^{2}}}}
is distributed according to the chi distribution. The chi distribution has one positive integer parameter
k
{\displaystyle k}
degrees of freedom (i.e. the number of random variables
Z
i
{\displaystyle Z_{i}}
The most familiar examples are the Rayleigh distribution (chi distribution with two degrees of freedom ) and the Maxwell–Boltzmann distribution of the molecular speeds in an ideal gas (chi distribution with three degrees of freedom).
Probability density function [ edit ] The probability density function (pdf) of the chi-distribution is
f
(
x
;
k
)
=
{
x
k
−
1
e
−
x
2
/
2
2
k
/
2
−
1
Γ
(
k
2
)
,
x
≥
0
;
0
,
otherwise
.
{\displaystyle f(x;k)={\begin{cases}{\dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}\Gamma \left({\frac {k}{2}}\right)}},&x\geq 0;\\0,&{\text{otherwise}}.\end{cases}}}
where
Γ
(
z
)
{\displaystyle \Gamma (z)}
gamma function .
Cumulative distribution function [ edit ] The cumulative distribution function is given by:
F
(
x
;
k
)
=
P
(
k
/
2
,
x
2
/
2
)
{\displaystyle F(x;k)=P(k/2,x^{2}/2)\,}
where
P
(
k
,
x
)
{\displaystyle P(k,x)}
regularized gamma function .
Generating functions [ edit ] The moment-generating function is given by:
M
(
t
)
=
M
(
k
2
,
1
2
,
t
2
2
)
+
t
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
M
(
k
+
1
2
,
3
2
,
t
2
2
)
,
{\displaystyle M(t)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {t^{2}}{2}}\right)+t{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {t^{2}}{2}}\right),}
where
M
(
a
,
b
,
z
)
{\displaystyle M(a,b,z)}
confluent hypergeometric function . The characteristic function is given by:
φ
(
t
;
k
)
=
M
(
k
2
,
1
2
,
−
t
2
2
)
+
i
t
2
Γ
(
(
k
+
1
)
/
2
)
Γ
(
k
/
2
)
M
(
k
+
1
2
,
3
2
,
−
t
2
2
)
.
{\displaystyle \varphi (t;k)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {-t^{2}}{2}}\right)+it{\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {-t^{2}}{2}}\right).}
The raw moments are then given by:
μ
j
=
∫
0
∞
f
(
x
;
k
)
x
j
d
x
=
2
j
/
2
Γ
(
1
2
(
k
+
j
)
)
Γ
(
1
2
k
)
{\displaystyle \mu _{j}=\int _{0}^{\infty }f(x;k)x^{j}\mathrm {d} x=2^{j/2}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+j)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}}
where
Γ
(
z
)
{\displaystyle \ \Gamma (z)\ }
gamma function . Thus the first few raw moments are:
μ
1
=
2
Γ
(
1
2
(
k
+
1
)
)
Γ
(
1
2
k
)
{\displaystyle \mu _{1}={\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+1)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}}
μ
2
=
k
,
{\displaystyle \mu _{2}=k\ ,}
μ
3
=
2
2
Γ
(
1
2
(
k
+
3
)
)
Γ
(
1
2
k
)
=
(
k
+
1
)
μ
1
,
{\displaystyle \mu _{3}=2{\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+3)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}=(k+1)\ \mu _{1}\ ,}
μ
4
=
(
k
)
(
k
+
2
)
,
{\displaystyle \mu _{4}=(k)(k+2)\ ,}
μ
5
=
4
2
Γ
(
1
2
(
k
+
5
)
)
Γ
(
1
2
k
)
=
(
k
+
1
)
(
k
+
3
)
μ
1
,
{\displaystyle \mu _{5}=4{\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k\!+\!5)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}=(k+1)(k+3)\ \mu _{1}\ ,}
μ
6
=
(
k
)
(
k
+
2
)
(
k
+
4
)
,
{\displaystyle \mu _{6}=(k)(k+2)(k+4)\ ,}
where the rightmost expressions are derived using the recurrence relationship for the gamma function:
Γ
(
x
+
1
)
=
x
Γ
(
x
)
.
{\displaystyle \Gamma (x+1)=x\ \Gamma (x)~.}
From these expressions we may derive the following relationships:
Mean:
μ
=
2
Γ
(
1
2
(
k
+
1
)
)
Γ
(
1
2
k
)
,
{\displaystyle \mu ={\sqrt {2\ }}\ {\frac {\ \Gamma \left({\tfrac {1}{2}}(k+1)\right)\ }{\Gamma \left({\tfrac {1}{2}}k\right)}}\ ,}
k
−
1
2
{\displaystyle {\sqrt {k-{\tfrac {1}{2}}\ }}\ }
k .
Variance:
V
=
k
−
μ
2
,
{\displaystyle V=k-\mu ^{2}\ ,}
1
2
{\displaystyle \ {\tfrac {1}{2}}\ }
k increases.
Skewness:
γ
1
=
μ
σ
3
(
1
−
2
σ
2
)
.
{\displaystyle \gamma _{1}={\frac {\mu }{\ \sigma ^{3}\ }}\left(1-2\sigma ^{2}\right)~.}
Kurtosis excess:
γ
2
=
2
σ
2
(
1
−
μ
σ
γ
1
−
σ
2
)
.
{\displaystyle \gamma _{2}={\frac {2}{\ \sigma ^{2}\ }}\left(1-\mu \ \sigma \ \gamma _{1}-\sigma ^{2}\right)~.}
The entropy is given by:
S
=
ln
(
Γ
(
k
/
2
)
)
+
1
2
(
k
−
ln
(
2
)
−
(
k
−
1
)
ψ
0
(
k
/
2
)
)
{\displaystyle S=\ln(\Gamma (k/2))+{\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi ^{0}(k/2))}
where
ψ
0
(
z
)
{\displaystyle \psi ^{0}(z)}
polygamma function .
Large n approximation [ edit ] We find the large n=k+1 approximation of the mean and variance of chi distribution. This has application e.g. in finding the distribution of standard deviation of a sample of normally distributed population, where n is the sample size.
The mean is then:
μ
=
2
Γ
(
n
/
2
)
Γ
(
(
n
−
1
)
/
2
)
{\displaystyle \mu ={\sqrt {2}}\,\,{\frac {\Gamma (n/2)}{\Gamma ((n-1)/2)}}}
We use the Legendre duplication formula to write:
2
n
−
2
Γ
(
(
n
−
1
)
/
2
)
⋅
Γ
(
n
/
2
)
=
π
Γ
(
n
−
1
)
{\displaystyle 2^{n-2}\,\Gamma ((n-1)/2)\cdot \Gamma (n/2)={\sqrt {\pi }}\Gamma (n-1)}
so that:
μ
=
2
/
π
2
n
−
2
(
Γ
(
n
/
2
)
)
2
Γ
(
n
−
1
)
{\displaystyle \mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {(\Gamma (n/2))^{2}}{\Gamma (n-1)}}}
Using Stirling's approximation for Gamma function, we get the following expression for the mean:
μ
=
2
/
π
2
n
−
2
(
2
π
(
n
/
2
−
1
)
n
/
2
−
1
+
1
/
2
e
−
(
n
/
2
−
1
)
⋅
[
1
+
1
12
(
n
/
2
−
1
)
+
O
(
1
n
2
)
]
)
2
2
π
(
n
−
2
)
n
−
2
+
1
/
2
e
−
(
n
−
2
)
⋅
[
1
+
1
12
(
n
−
2
)
+
O
(
1
n
2
)
]
{\displaystyle \mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {\left({\sqrt {2\pi }}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot [1+{\frac {1}{12(n/2-1)}}+O({\frac {1}{n^{2}}})]\right)^{2}}{{\sqrt {2\pi }}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+{\frac {1}{12(n-2)}}+O({\frac {1}{n^{2}}})]}}}
=
(
n
−
2
)
1
/
2
⋅
[
1
+
1
4
n
+
O
(
1
n
2
)
]
=
n
−
1
(
1
−
1
n
−
1
)
1
/
2
⋅
[
1
+
1
4
n
+
O
(
1
n
2
)
]
{\displaystyle =(n-2)^{1/2}\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]={\sqrt {n-1}}\,(1-{\frac {1}{n-1}})^{1/2}\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}
=
n
−
1
⋅
[
1
−
1
2
n
+
O
(
1
n
2
)
]
⋅
[
1
+
1
4
n
+
O
(
1
n
2
)
]
{\displaystyle ={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{2n}}+O({\frac {1}{n^{2}}})\right]\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}
=
n
−
1
⋅
[
1
−
1
4
n
+
O
(
1
n
2
)
]
{\displaystyle ={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}
And thus the variance is:
V
=
(
n
−
1
)
−
μ
2
=
(
n
−
1
)
⋅
1
2
n
⋅
[
1
+
O
(
1
n
)
]
{\displaystyle V=(n-1)-\mu ^{2}\,=(n-1)\cdot {\frac {1}{2n}}\,\cdot \left[1+O({\frac {1}{n}})\right]}
If
X
∼
χ
k
{\displaystyle X\sim \chi _{k}}
X
2
∼
χ
k
2
{\displaystyle X^{2}\sim \chi _{k}^{2}}
chi-squared distribution )
χ
1
∼
H
N
(
1
)
{\displaystyle \chi _{1}\sim \mathrm {HN} (1)\,}
half-normal distribution ), i.e. if
X
∼
N
(
0
,
1
)
{\displaystyle X\sim N(0,1)\,}
|
X
|
∼
χ
1
{\displaystyle |X|\sim \chi _{1}\,}
Y
∼
H
N
(
σ
)
{\displaystyle Y\sim \mathrm {HN} (\sigma )\,}
σ
>
0
{\displaystyle \sigma >0\,}
Y
σ
∼
χ
1
{\displaystyle {\tfrac {Y}{\sigma }}\sim \chi _{1}\,}
χ
2
∼
R
a
y
l
e
i
g
h
(
1
)
{\displaystyle \chi _{2}\sim \mathrm {Rayleigh} (1)\,}
Rayleigh distribution ) and if
Y
∼
R
a
y
l
e
i
g
h
(
σ
)
{\displaystyle Y\sim \mathrm {Rayleigh} (\sigma )\,}
σ
>
0
{\displaystyle \sigma >0\,}
Y
σ
∼
χ
2
{\displaystyle {\tfrac {Y}{\sigma }}\sim \chi _{2}\,}
χ
3
∼
M
a
x
w
e
l
l
(
1
)
{\displaystyle \chi _{3}\sim \mathrm {Maxwell} (1)\,}
Maxwell distribution ) and if
Y
∼
M
a
x
w
e
l
l
(
a
)
{\displaystyle Y\sim \mathrm {Maxwell} (a)\,}
a
>
0
{\displaystyle a>0\,}
Y
a
∼
χ
3
{\displaystyle {\tfrac {Y}{a}}\sim \chi _{3}\,}
‖
N
i
=
1
,
…
,
k
(
0
,
1
)
‖
2
∼
χ
k
{\displaystyle \|{\boldsymbol {N}}_{i=1,\ldots ,k}{(0,1)}\|_{2}\sim \chi _{k}}
Euclidean norm of a standard normal random vector of with
k
{\displaystyle k}
k
{\displaystyle k}
degrees of freedom chi distribution is a special case of the generalized gamma distribution or the Nakagami distribution or the noncentral chi distribution
lim
k
→
∞
χ
k
−
μ
k
σ
k
→
d
N
(
0
,
1
)
{\displaystyle \lim _{k\to \infty }{\tfrac {\chi _{k}-\mu _{k}}{\sigma _{k}}}{\xrightarrow {d}}\ N(0,1)\,}
Normal distribution )The mean of the chi distribution (scaled by the square root of
n
−
1
{\displaystyle n-1}
unbiased estimation of the standard deviation of the normal distribution .
Various chi and chi-squared distributions
Name
Statistic
chi-squared distribution
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}
noncentral chi-squared distribution
∑
i
=
1
k
(
X
i
σ
i
)
2
{\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}
chi distribution
∑
i
=
1
k
(
X
i
−
μ
i
σ
i
)
2
{\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}}
noncentral chi distribution
∑
i
=
1
k
(
X
i
σ
i
)
2
{\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}}
Martha L. Abell, James P. Braselton, John Arthur Rafter, John A. Rafter, Statistics with Mathematica (1999), 237f.
Jan W. Gooch, Encyclopedic Dictionary of Polymers vol. 1 (2010), Appendix E, p. 972 .
Discrete
with finite with infinite
Continuous
supported on a supported on a supported with support
Mixed
Multivariate Directional Degenerate singular Families
















































![{\displaystyle \mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {\left({\sqrt {2\pi }}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot [1+{\frac {1}{12(n/2-1)}}+O({\frac {1}{n^{2}}})]\right)^{2}}{{\sqrt {2\pi }}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+{\frac {1}{12(n-2)}}+O({\frac {1}{n^{2}}})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ab2d5763ab73955d1da591a2c76909c453fb48)
![{\displaystyle =(n-2)^{1/2}\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]={\sqrt {n-1}}\,(1-{\frac {1}{n-1}})^{1/2}\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f3e1534e28ac6e9276477260c929f0fa2072a4e)
![{\displaystyle ={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{2n}}+O({\frac {1}{n^{2}}})\right]\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f137a4f4c36c6d1a3e6e133d9ea9c8cf4cc3cfa)
![{\displaystyle ={\sqrt {n-1}}\,\cdot \left[1-{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16110f5e6cee819cf7ce548062a398bcf57f7eac)
![{\displaystyle V=(n-1)-\mu ^{2}\,=(n-1)\cdot {\frac {1}{2n}}\,\cdot \left[1+O({\frac {1}{n}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5610836c34d335011ebc02dc4ee6ec6753aac429)





















